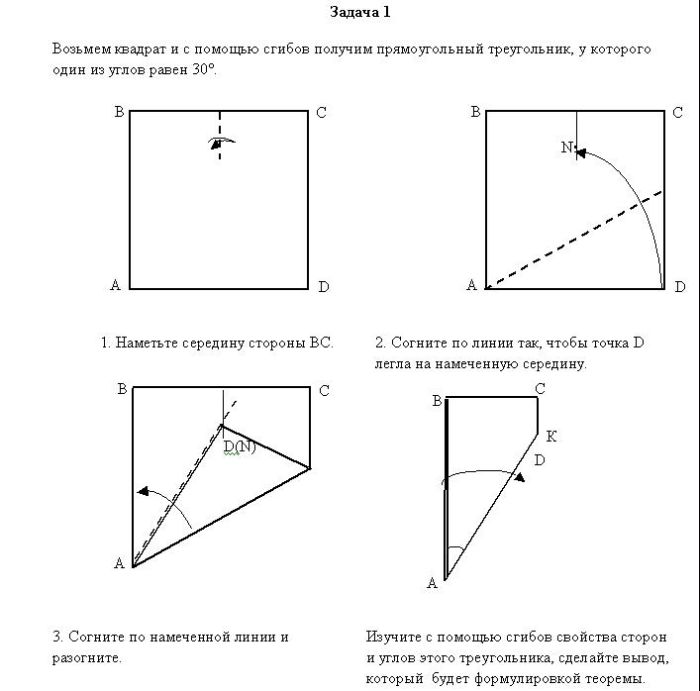
Как у нас проходил Творческий этап конкурса ДООМ "Оригами и геометрия" - 2008
Мы складывали, доказывали, спорили, снова складывали и доказывали, получили много новых для нас интересных свойств геометрических фигур.
 |
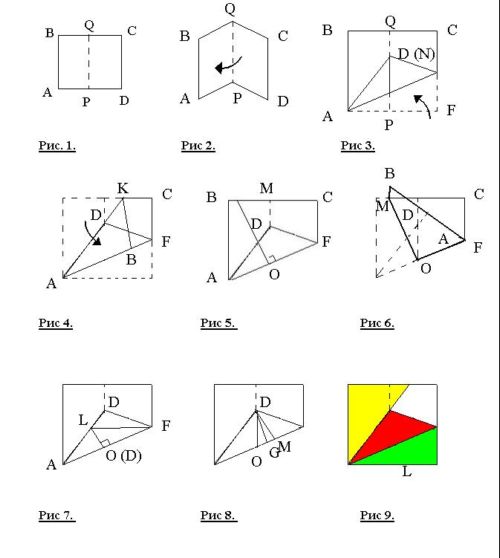
Оригамское решение (исследование)Задача (а). 1 шаг. Возьмём квадратный лист бумаги ABCD (рис. 1). 2 шаг. Сложим бумажный лист пополам, сторона AB к стороне CD . 3 шаг. Развернём образовавшуюся серединную складку QP (рис. 2). 4 шаг. Загнём бумагу по линии AF таким образом, чтобы вершина D наложилась на линию QP (рис. 3). 5 шаг. Вывод : L ADF прямоугольный, т.к. L A - угол квадрата. 6 шаг. Отметим точку N на отрезке QP совпадающую с точкой D при наложении. 7 шаг. Треугольник ADF равен треугольнику ANF т.к. совпали при наложении, и L DAF = L NAF . 8 шаг. Загнём треугольник с вершиной B по линии AK поверх треугольника ADF (рис.4). 9 шаг. Образовавшиеся три угла при вершине A при наложении совпадают, следовательно равны 1\3 части LА, т. е. 30 о . Вывод L DAF=30 о 10 шаг. Развернём угол квадрата В. 11 шаг. Загнём по линии ОМ бумагу так, чтобы угол В А O совпадал с углом D F О (рис. 5,6) и сделаем вывод , что L DFA =L BAF = 60, как 2/3 LА квадрата. Второй вывод , что сумма острых углов в прямоугольном треугольнике равна 90, у нас один угол равен 30, следовательно другой - 60. 12 шаг. Отменим предыдущую операцию. Точка О делит отрезок AF пополам (по построению). 13 шаг. Отогнём вершину L D по линии FL . Точка D совпала с точкой О, т.е DF = FO =1/2 AF (рис. 7). Вывод: в прямоугольном треугольнике напротив угла в 30 о лежит катет, равный половине гипотенузы. Задача (б). 14 шаг. Опустим из вершины прямого угла D высоту на гипотенузу AF для этого перегнем бумагу по линии DH так, чтобы нижние края совместились, т.е. образовали угол 90, следовательно DH – высота, причём точка F совпадёт с точкой O . 15 шаг. Треугольник ODH будет равнобедренным, OH = HF =1/4 AF . 16 шаг. Вывод: высота, опушенная из прямого угла прямоугольного треугольника с углом в 30, отсекает 1/4 часть гипотенузы, начиная от вершины большого угла, а медиана равна катету, лежащему против угла в 30. 17 шаг . Треугольник ODF – равносторонний. 18 шаг. Вывод: медиана и высота, проведённые из прямого угла в прямоугольном треугольнике с углом в 30 о , делят угол на три равных угла по 30. 19 шаг. Биссектриса L ADF разделит так же и L ODH пополам, т.е. угол между высотой и медианой (легко проверить, сложив угол пополам). Вывод биссектриса, проведенная из прямого угла в треугольнике с углом в 30, является биссектрисой угла между медианой и высотой проведенной из этого же угла (рис. 8). 20 шаг. Развернем квадрат – складки образуют 3 равных треугольника (рис.9). Вывод из задачи. Данным способом можно делить прямой угол и сторону квадрата на три равных части. Точка L производит это деление. LO = 1/2 LF (т.к. D LOF – прямоугольный с углом в 30), LF = LA (т.к. треугольник ALF - равнобедренный по признаку равенства двух углов), следовательно DL = 1/3 DA (рис.7) |
|---|---|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |

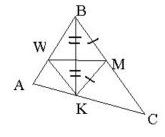
Оригамское решение1 шаг. Возьмем и вырежем из бумаги произвольный треугольник. Обозначим его вершины A , B , C . За угол B можно принять любой произвольный угол (тупой, острый или прямой). 2 шаг. Разделим L ABC пополам, совместим линии сторон BC и BA , намеченная линия сгиба и есть биссектриса (BK), т.к. углы при наложении совпадут. 3 шаг. Необходимо на стороне BC найти местоположение для точки M , зная, что BM = MK; т.е. она должна быть равноудалена от точек B и K и, следовательно, находится на серединном перпендикуляре к отрезку BK. Совместим точки B и K и замнём складку, она будет являться серединным перпендикуляром и пересечёт сторону BC в искомой точке M. 4 шаг. Наметим линию MK . 5 шаг. Чтобы доказать, что KM || AB , необходимо через любую точку между K и C перегнуть треугольник так, чтобы сторона AB совместилась по своему краю. Заметим, сто при этом части отрезка MK наложатся друг на друга (две прямые, перпендикулярные третьей прямой, параллельны).
Дано: Треугольник АВС: ВК – биссектриса, ВМ = МК Доказать: КМ||АВ. Доказательство: L АВК = L КВМ (по определению биссектрисы) L КВМ = L ВКМ (по свойству углов при основании равнобедренного треугольника) По транзитивности имеем, L АВК = L ВКМ, данные углы являются накрест лежащими при прямых АВ и КМ секущей ВК, т. к. они равны, то по признаку параллельных прямых имеем КМ||АВ. Что и требовалось доказать. |
 |
||
 |
|||
 |
|||
 |